Prim’s Algorithm in C

Prim’s Algorithm is an approach to determine minimum cost spanning tree. In this case, we start with single edge of graph and we add edges to it and finally we get minimum cost tree. In this case, as well, we have n-1 edges when number of nodes in graph are n.We again and again add edges to tree and tree is extended to create spanning tree, while in case of Kruskal’s algorithm there may be more than one tree, which is finally connected through edge to create spanning tree.

Algorithm

This algorithm creates spanning tree with minimum weight from a given weighted graph.

1. Begin
2. Create edge list of given graph, with their weights.
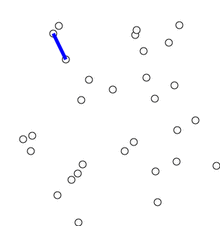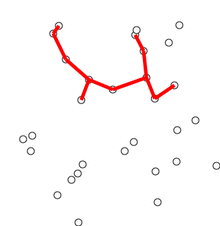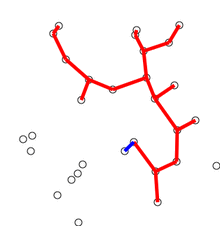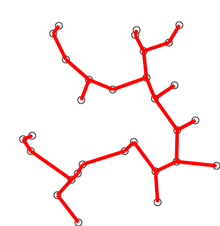
3. Draw all nodes to create skeleton for spanning tree.
4. Select an edge with lowest weight and add it to skeleton and delete edge from edge list.
5. Add other edges. While adding an edge take care that the one end of the edge should always be in the skeleton tree and its cost should be minimum.
6. Repeat step 5 until n-1 edges are added.
7. Return.

C program for constructing a minimum cost spanning tree of a graph using Prim’s algorithm 

#include<stdio.h>
#include<stdlib.h>
 
#define infinity 9999
#define MAX 20
 
int G[MAX][MAX],spanning[MAX][MAX],n;
 
int prims();
 
int main()
{
    int i,j,total_cost;
    printf("Enter no. of vertices:");
    scanf("%d",&n);
    
    printf("\nEnter the adjacency matrix:\n");
    
    for(i=0;i<n;i++)
        for(j=0;j<n;j++)
            scanf("%d",&G[i][j]);
    
    total_cost=prims();
    printf("\nspanning tree matrix:\n");
    
    for(i=0;i<n;i++)
    {
        printf("\n");
        for(j=0;j<n;j++)
            printf("%d\t",spanning[i][j]);
    }
    
    printf("\n\nTotal cost of spanning tree=%d",total_cost);
    return 0;
}
 
int prims()
{
    int cost[MAX][MAX];
    int u,v,min_distance,distance[MAX],from[MAX];
    int visited[MAX],no_of_edges,i,min_cost,j;
    
    //create cost[][] matrix,spanning[][]
    for(i=0;i<n;i++)
        for(j=0;j<n;j++)
        {
            if(G[i][j]==0)
                cost[i][j]=infinity;
            else
                cost[i][j]=G[i][j];
                spanning[i][j]=0;
        }
        
    //initialise visited[],distance[] and from[]
    distance[0]=0;
    visited[0]=1;
    
    for(i=1;i<n;i++)
    {
        distance[i]=cost[0][i];
        from[i]=0;
        visited[i]=0;
    }
    
    min_cost=0;        //cost of spanning tree
    no_of_edges=n-1;        //no. of edges to be added
    
    while(no_of_edges>0)
    {
        //find the vertex at minimum distance from the tree
        min_distance=infinity;
        for(i=1;i<n;i++)
            if(visited[i]==0&&distance[i]<min_distance)
            {
                v=i;
                min_distance=distance[i];
            }
            
        u=from[v];
        
        //insert the edge in spanning tree
        spanning[u][v]=distance[v];
        spanning[v][u]=distance[v];
        no_of_edges--;
        visited[v]=1;
        
        //updated the distance[] array
        for(i=1;i<n;i++)
            if(visited[i]==0&&cost[i][v]<distance[i])
            {
                distance[i]=cost[i][v];
                from[i]=v;
            }
        
        min_cost=min_cost+cost[u][v];
    }
    
    return(min_cost);
}

Output

Enter no. of vertices:6

Enter the adjacency matrix:
0 3 1 6 0 0
3 0 5 0 3 0
1 5 0 5 6 4
6 0 5 0 0 2
0 3 6 0 0 6
0 0 4 2 6 0

spanning tree matrix:
0 3 1 0 0 0
3 0 0 0 3 0
1 0 0 0 0 4
0 0 0 0 0 2
0 3 0 0 0 0
0 0 4 2 0 0

Total cost of spanning tree=13